What did scientists discover?
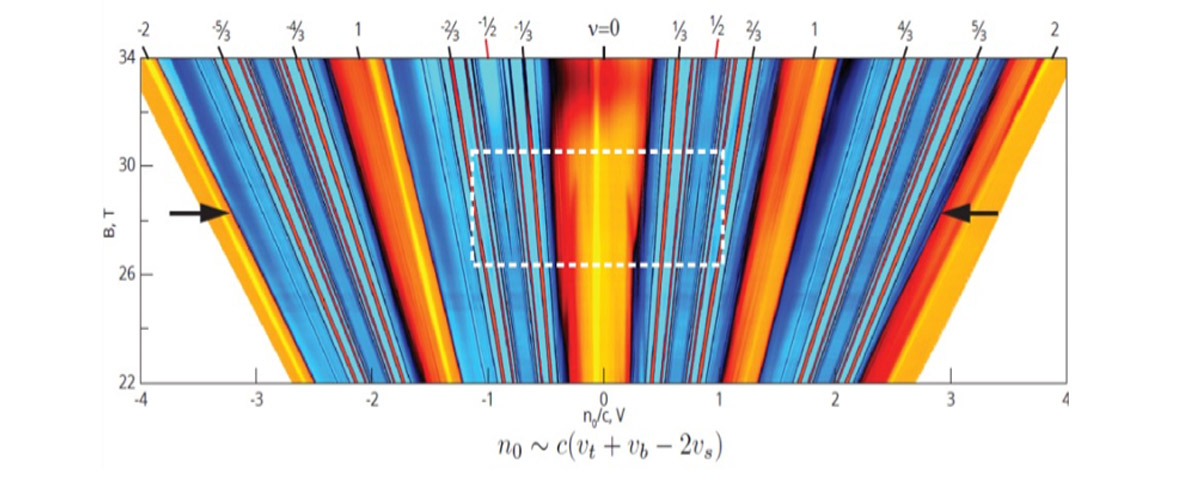
Fractional quantum Hall (FQH) states are topological, insulating states in which the electron-electron interaction results in a quasiparticle that behaves as if it only has a fraction of the charge normally carried by a free electron. In a single layer of graphene, scientists observed a new and unexpected class of FQH states that occur within a narrow range of magnetic fields around 28 teslas.
Why is this important?
FQH states are one of the most striking effects of electron interactions. Some exhibit properties that could be exploited for quantum computation. This discovery showcases the potential for engineering new properties by tuning, or manipulating, graphene using electric and magnetic fields.
Who did the research?
A. A. Zibrov1, E.M. Spanton1, H. Zhou1, C. Kometter1, T. Taniguchi2, K. Watanabe2, A.F. Young1
1University of California, Santa Barbara; 2National Institute for Materials Science
Why did they need the MagLab?
In many samples, the new FQH states only occur for a narrow range of high magnetic fields, up to 30 tesla. Additionally, temperatures below 1 kelvin are required to observe the most fragile of these quantum mechanical states.
Details for scientists
- View or download the expert-level Science Highlight, Even-denominator fractional quantum Hall states at an isospin transition in monolayer graphene
- Read the full-length publication, Even-denominator fractional quantum Hall states at an isospin transition in monolayer graphene, in Nature Physics
Funding
This research was funded by the following grants: G.S. Boebinger (NSF DMR-1157490); A.F. Young(NSF DMR-1654186, ARO 69188PHH)
For more information, contact Tim Murphy.